Senin, 26 November 2012
rumus dasar :
![\int_{a}^{b}f(x)dx=[F(x)]_{a}^{b}=F(b)-F(a)](http://latex.codecogs.com/gif.latex?\int_{a}^{b}f(x)dx=[F(x)]_{a}^{b}=F(b)-F(a))
contoh:
![\int_{-2}^{3}(2x^{2}+3x-5)dx=[(\frac{2}{3}x^{3}+\frac{3}{2}x^{2}-5x)]_{-2}^{3}](http://latex.codecogs.com/gif.latex?\int_{-2}^{3}(2x^{2}+3x-5)dx=[(\frac{2}{3}x^{3}+\frac{3}{2}x^{2}-5x)]_{-2}^{3})
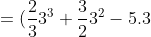-(\frac{2}{3}-2^{3}+\frac{3}{2}-2^{2}-5.-2))
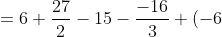+10)
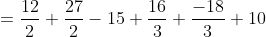

Gambar 1.
Luas daerah di atas sumbu-x

Gambar 2.
Luas daerah di bawah sumbu x

Gambar 4. Luas daerah yang terletak
di antara dua kurva
Contoh Soal:

contoh:
= (itung sendiri ya :p)
menghitung luas
Misalkan R daerah yang dibatasi oleh kurva y = f(x), sumbu-x, garis x = a, dan garis x = b, dengan f(x) > 0 pada [a, b], maka luas daerah R adalah sebagai berikut.

Gambar 1.
Luas daerah di atas sumbu-x
Contoh Soal:
Misalnya S daerah yang dibatasi oleh kurva y = f(x), sumbu-x, garis x = a, dan garis x = b, dengan f(x) < 0 pada [a, b], maka luas daerah S adalah:

Gambar 2.
Luas daerah di bawah sumbu x
Contoh Soal:
Gambar 3.
Luas daerah yang dibatasi kurva y = f(x) dan sumbu-xContoh Soal:
Luas daerah U pada gambar di bawah adalah: L(U) Luas ABEF - Luas ABCD

Gambar 4. Luas daerah yang terletak
di antara dua kurva
ABEF adalah daerah yang dibatasi oleh kurva y1 = f(x), x = a, x = b, dan y = 0 sehingga
Contoh Soal:

Langganan:
Posting Komentar (Atom)








0 komentar:
Posting Komentar